Methods in Reliability
I am describing below concepts in reliability the reader might find interesting to think about and realise. In reliability we focus on the probability of a system to operate without failure over a given period of time.
Positioning of Reliability
From a philosophical standpoint, I would argue that reliability is related or linked to actuarial sciences. The interest or the estimation of the probability of failure over time of an entity is shared by both. In life-insurance, we are using mortality tables to calculated relevant probabilities. For lifetime analysis, we might opt for a parametric or non-parametric option.
The reliability of products is closely linked to the study of their durability and survival analysis.
The area of applied statistics in industry encompasses various branches. As one of the most used could be mentioned quality control and in particular, the use of t-tests. Among many other tests to address, whether a sample meets the assumed quality or characteristics.
A common feature in lifetime data is the presence of censoring. It describes the situation, when we miss observing a part of the lifetime. Most commonly having to end the experiment prematurely, for time constraints, even though not having observed all components. Therefore, we do assume that these components would last some time longer. The methods incorporate the presence of censoring and make use of this information.
Companies deal with reliability for example in maintenance problems. When is the right time to change parts of the equipment, leading to an optimisation problem. There are some financial burdens connected with performing check and changing equipment. However, fall out of the functionality of the whole system could be costly and worse.
Definitions
Continuing with the basic definitions, let us describe the distribution function as F(x)=P(X<x) describing a random variable (e.g. wheel bearing) X in the way of addressing the probability that the time to failure is smaller than x.
The survival function S(x) is the complement to the distribution function S(x)=1-F(x).
We call the survival function also the reliability function. It describes the probability that a random variable lasts at least until time x.
A special function that is introduced in reliability is the hazard function. It links to the survival function in the way
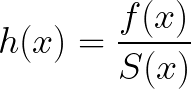
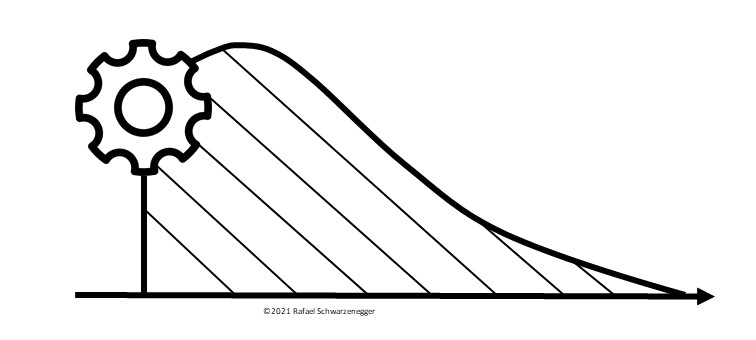
For a system the hazard function is forming a bathtub curve as described in (Karpíšek, 2005; Schwarzenegger, 2017)
One of possible bathtub curves is depicted above. It consists of 3 stages, namely infant mortality, useful life and wear out life.
If systems are analysed and we focus on finding the weakest link in a chain of components, we will be using fault trees. Illustrating with a simple example of a system of 2 light bulbs connected with electrified wire. If we have a series setup as in figure 1, the reliability of the system will be calculated as the product of the components R_1*R_2. Complementary, the probability of failure of the system is the sum of the component failure probabilities F_1+F_2. To prove, R= R_1*R_2=(1-F_1)*(1-F_2). For a parallel system in figure B, the reliability of the system will be calculated as the sum of the underlying component reliabilities R_1+R_2 (supportive reading in here). Intuitively a redundant system leads to more reliability. Therefore a sum will produce a higher reliability that a product those 2 numbers.
In a fault tree, the series system is represented with an OR gate and the parallel system with an AND gate. For more complex situations, we might more advanced gates like the "voting OR gate" where only some components can fail and the system is still working.
It usually handy from a logical standpoint to transform the logical relationships into the conjunctive AND or OR form (science direct link). So all logical relationships, may be decomposed into AND and OR relationships. For example A implying B is equivalent to notA "OR" B. There are much more logical equivalences. Moreover do not even need to gates. All gates may be transformed into a NAND (notAND) gate. This is, how in informatics computers work. One gate type would be enough to work with.
Please read this blog post as well on the StrathLife PGR Blog.